动态调整运行代价的核心原理是通过实时感知系统状态,将环境负载、资源占用等动态因素转化为路径规划或任务调度的代价增量,从而引导系统资源向低负载区域分配,实现负载均衡与效率优化。以下是其实现原理的详细解析:
传统代价模型:在路径规划(如A*算法)中,代价通常仅包含距离、转向角度等静态因素,导致高负载区域因路径短而被频繁选择,引发拥堵。
动态代价模型:引入与系统状态相关的动态因子(如区域AGV密度、任务队列长度),将负载信息转化为代价增量,使算法优先选择低负载路径。
数学表达:
传统代价:g(x)=l(x)(仅距离代价)
动态代价:(x)=l(x)+fdynamic(load(x))(距离+动态负载代价)其中,fdynamic
为负载到代价的映射函数。
负载统计单元:将连续空间划分为离散区域(如网格、路段),统计每个区域的实时负载(如AGV数量、任务积压量)。
数据来源:
直接感知:通过AGV上报位置、速度等数据。
间接推断:根据任务完成时间、通信延迟等间接指标估算负载。
更新频率:高频更新(如每秒1次)以捕捉瞬态变化,低频更新(如每分钟1次)以减少计算开销。
示例:
在仓库中,将地面划分为1m×1m网格,每个网格维护一个计数器,记录过去10秒内经过的AGV数量。
线性映射:
fdynamic(load)=α⋅load适用于负载变化平缓的场景,α 为权重系数。
非线性映射:
指数模型:
fdynamic(load)=βeγload
分段函数:
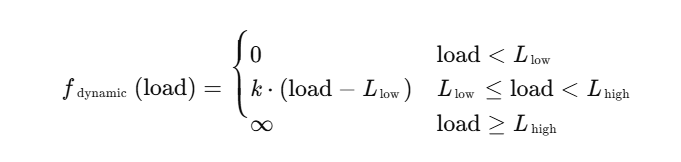
| 强制避开超载区域。 |
参数选择:
通过仿真或实验确定 α,β,γ,例如在10×10路网中,α=0.5 可平衡路径长度和负载均衡。
路径规划算法:在A*、Dijkstra等算法中,将动态代价作为节点扩展的评估标准。
开放列表更新:每次从开放列表中选取 f(x)=g(x)+h(x) 最小的节点,其中 g(x) 包含动态代价。
闭环反馈:路径规划完成后,更新路网负载数据,影响后续决策。
任务调度算法:在任务分配时,将动态代价作为任务-资源匹配的优先级指标。
伪代码示例(A*算法修改):
def dynamic_astar(start, goal, load_monitor, alpha=0.5): open_set = PriorityQueue() open_set.put(start, 0) g_score = {start: 0}
while not open_set.empty(): current = open_set.get() if current == goal: return reconstruct_path()
for neighbor in get_neighbors(current): # 动态代价:距离 + 负载惩罚 distance_cost = euclidean_distance(current, neighbor) load_cost = alpha * load_monitor.get_load(neighbor.grid_id) tentative_g = g_score[current] + distance_cost + load_cost
if neighbor not in g_score or tentative_g < g_score[neighbor]: g_score[neighbor] = tentative_g open_set.put(neighbor, tentative_g + heuristic(neighbor, goal)) return None
开环系统:传统路径规划无负载反馈,导致拥堵。
闭环系统:动态代价引入负反馈,当某区域负载升高时,其代价增加,促使后续路径避开该区域,形成自动均衡。
类比:
类似交通信号灯根据车流量动态调整时长,避免路口拥堵。
纳什均衡:每个AGV作为理性个体,选择最小化自身代价的路径,动态代价函数引导个体行为趋向系统最优。
价格机制:负载代价类似“拥堵税”,高负载区域的高代价迫使AGV选择其他路径。
时间维度:通过动态代价调整路径选择时序,避免多AGV同时进入同一区域。
空间维度:将负载分散到不同物理区域,减少局部冲突。
负载均衡:避免热点区域过载,提升系统吞吐量。
鲁棒性增强:对突发任务或设备故障更具适应性。
效率优化:在保证均衡的前提下,尽量缩短路径长度。
计算开销:高频负载更新和动态代价计算可能增加系统负担。
参数调优:负载权重 α 需根据场景调整,缺乏普适性。
数据延迟:负载感知延迟可能导致决策滞后,需优化数据采集与传输。
AGV仓储系统:动态调整路径代价,避免充电站、交叉口等区域拥堵。
交通信号控制:根据车流量动态调整绿灯时长,优化路口通行效率。
云计算资源分配:根据虚拟机负载动态调整任务调度优先级。
动态调整运行代价的实现原理可概括为:
“实时感知系统状态 → 将状态映射为代价增量 → 通过代价函数引导决策 → 形成负反馈闭环”。
其本质是通过数学建模将物理世界的负载分布转化为算法可优化的数字信号,最终实现资源的高效、均衡利用。
